数据结构之跳跃表
目录
简介
跳跃表(skiplist)是一种有序数据结构,它通过在每个节点中维持多个指向其他节点指针,从而达到快速访问节点的目的。
针对数组,我们可以使用二分查找算法在O(log(N))的时间查找到目标, 但它受限于数组这种数据结构。那如果是链表结构,能否达到类似”二分“查找的效果呢?实际上,跳表就是对链表的一种改造,使之有了类似”二分“查找的效果。
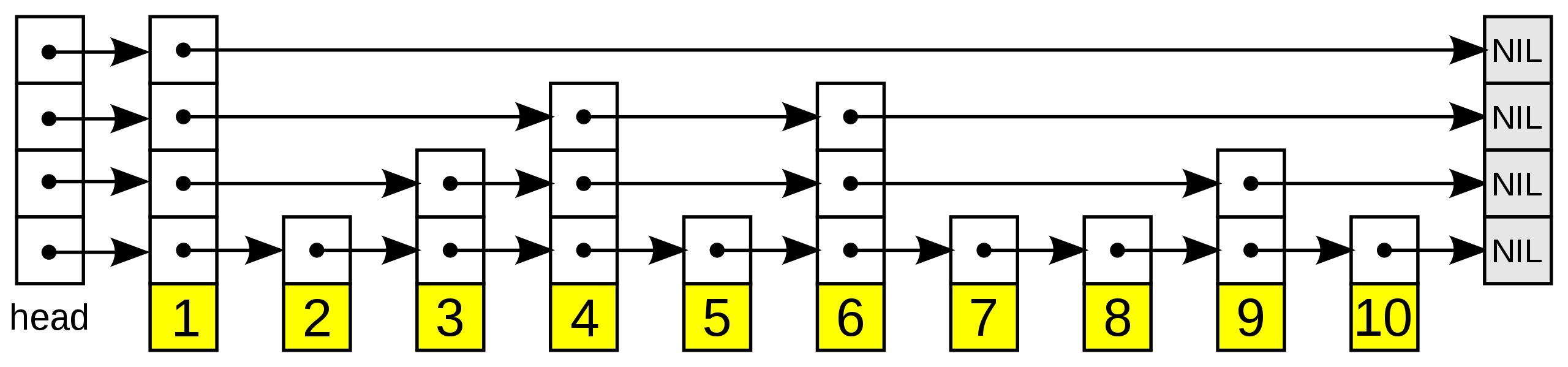
一张跳跃列表的示意图。每个带有箭头的框表示一个指针, 而每行是一个稀疏子序列的链表;底部的编号框(黄色)表示有序的数据序列。查找从顶部最稀疏的子序列向下进行, 直至需要查找的元素在该层两个相邻的元素中间。
查找
查找一个目标元素,从顶层列表和头元素起步,并沿着每层链表搜索。如果在一层列表中找到的元素等于目标元素,则表明该元素直接被找到。当在一层列表中查找到小于目标的元素时,就切换至该元素继续向右或向下层查找,直至底层链表。查找的时间复杂度O(log(N))。
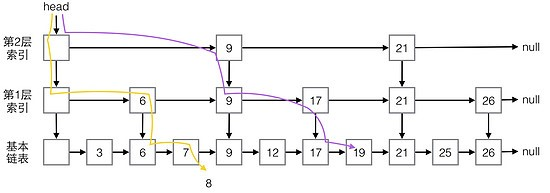
这是网上找到的演示查找过程的一张图,其中紫色线表示查找19这个元素的过程,黄色线表示找8这个元素的过程。
插入删除
对于跳跃表的插入和删除都很好理解,分为两个步骤。1.查找到插入删除位置(O(log(n))的时间);2.执行插入删除操作( O(1)时间 )。总的时间复杂度为(log(n)) 。
索引动态更新
当大量的新节点插入到原链表之后,上层的索引节点会慢慢变得不够用。这时候需要选取一部分提到上层,那如何选择呢?跳表采用的是随机提拔的方法,通过一个随机函数,对于新加入的节点,由计算的随机值要决定是否将它加入(提拔)到索引层。
时间空间复杂度汇总
时间复杂度
- 查找:O(log(n))
- 插入:O(log(n))
- 删除:O(log(n))
空间复杂度:O(n)
跳跃表高度:O(log(n))
相较于平衡二叉树的优点
- 虽然插入、删除、查找以及迭代输出有序序列这几个操作红黑树也可以实现,且复杂度一样。但按照区间查找数据这个操作,红黑树的效率没有跳表高。
- 跳表更容易代码实现。
- 维护结构平衡的成本比较低,完全依靠随机。而二叉查找树在多次插入删除后,需要Rebalance来重新调整结构平衡。
跳表的具体实现
- Redis的有序集合采用跳表实现,具体实现可查看文章Redis数据结构:跳表